2023级算法C1上机赛

2023级算法C1上机赛

Tengpaz Lv3
  2024-09-14 17:02:36 2024-09-14 17:02:36 创建   2024-10-07 11:19:51 2024-10-07 11:19:51 更新      

2023级软院学生第一次上机赛习题讲解

补题情况

2024ALC1

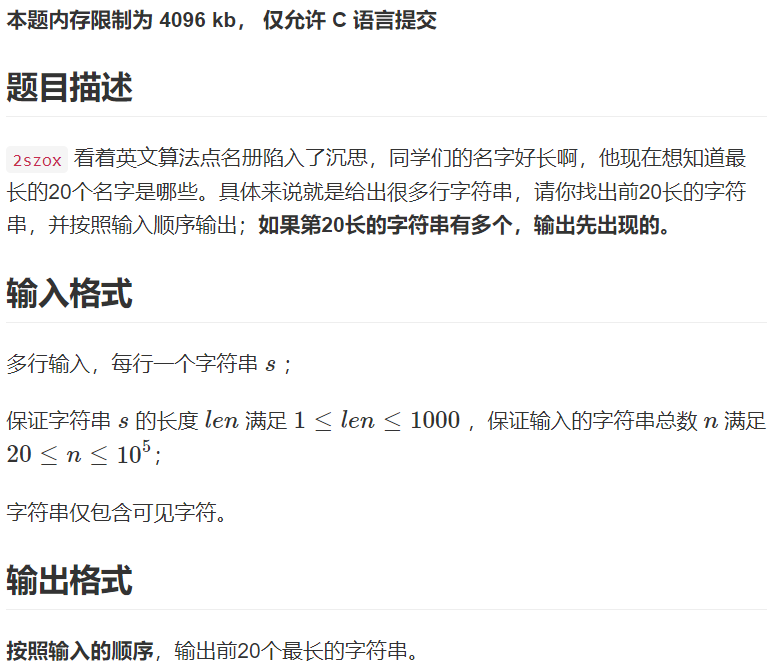
C 最长的姓名

原题如下

2024ALC1C

你需要知道

  • 快排函数的使用/快排的实现
  • 插入排序的实现
  • 内存压缩
  • 多关键字排序

解题思路

首先看清题目要求，本题内存限制为 4096 kb， 仅允许 C 语言提交

本人上来要求不看畅快写了一篇cpp代码，成功获得没有可提交语言的快乐.

大致浏览题目信息，可以不难知道，本题特地禁止使用了C++的STL，并且加上了内存的限制范围，所以一开始思路就要放在这几个方面：

  1. 减少内存占用，所以必然不能存下所有字符串后进行统一排序处理，这样避免了用内存换取时间
  2. 既然禁用了C++STL，将计就计参考这个实现思路，实现C++的set容器实现逻辑，即对于已有的符合题目需求的答案字符串需要维护字符串长度顺序，这里时间宽泛数据量小，根据数据逐个获取处理的特征，选择插入排序进行维护，同时对于旧有的被顶替的答案，合理清除，这里选择只定义长度有限的字符串数组，排序后超出长度外的数据自然抛弃
  3. 题目要求按照原始输入顺序进行输出，于是还需要最后还原输入顺序，以及在之前的排序情况下，对于数组的维护既要维护长度次序，又要维护输入顺序这个次要关键字的顺序

插入排序&内存压缩

大致实现就像你手中已经有了一列牌，牌已经按照一定顺序（这里全部默认为由小到大排序），此时你拿了一张牌，需要插入已有牌堆，且不破坏牌堆顺序

不难想到可以依次从小到大比较新牌与牌堆中牌的大小，直到发现第一张比新牌大的牌，于是将新牌插入这张牌前面，实现插入排序。

当然也有可能找到末尾还没有更大的牌了，此时直接插入牌尾。

同理，这道题需要实现对于20个字符串的长度顺序的维持，由于考虑空间限制，我们自然不能够将所有字符串全部获取后来个快排干脆利落地解决，需要动态维护，时间要求不高，直接用简单的插入已经完全够了。

存在两种情况，在获取到20个字符串前，对于获得的字符串只需要无脑插入排序到答案字符串数组里。

在已经获取到了20个字符串后，此时需要做的不仅是插入，还有删除。

所以在找到插入位置后，需要对于找到的位置进行判断，如果是如上面案例中第二种情况，已经找到数组尾部，还没有发现比手中字符串长的字符串，这里需要直接舍弃。

其它情况只需要忽略最后一个字符串，将前面至插入位的字符串后移一位，自然末位淘汰。

实际代码中我添加了一个多余的数组格，也就是我保留了21个元素，这样用来处理舍弃情况，因为如果搜寻到了第21位，直接进行舍弃即可。

多关键字

由于最后题目要求按照输入顺序输出，所以还需要保留字符串的输入顺序信息，最后根据这个关键字再一次进行排序，由于只有29个元素，任意排序方式都能河里通过。这里使用快排函数。

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
/* 
 Author: 王宇祯
 Result: AC	Submission_id: 6316128
 Created at: Wed Sep 11 2024 20:14:37 GMT+0800 (China Standard Time)
 Problem_id: 8189	Time: 29	Memory: 1540
*/

#include<stdio.h>
#include<string.h>
#include<stdlib.h>

typedef struct string {
    int len;
    int id;
    char str[1001];
} string_;

string_ strings[21] = {0};
int content = 0;

int cmp2(const void* a, const void* b) {
    string_* aa = (string_*)a;
    string_* bb = (string_*)b;
    if (aa->id > bb->id) return 1;
    if (aa->id < bb->id) return -1;
}

int main() {
    int n = 0;
    string_ str;
    while (gets(str.str) != NULL) {
        str.id = n;
        str.len = strlen(str.str);
        if (content == 0) {
            strings[content++] = str;
        } else if (content <= 19) {
            int i = 0;
            for (i = 0; i < content; i++) {
                if (strings[i].len < str.len) {
                    for (int j = content; j > i; j--) {
                        strings[j] = strings[j - 1];
                    }
                    strings[i] = str;
                    content++;
                    break;
                }
            }
            if (i == content) {
                strings[content++] = str;
            }
        } else {
            int i = 0;
            for (i = 0; i < content; i++) {
                if (strings[i].len < str.len) {
                    for (int j = content; j > i; j--) {
                        strings[j] = strings[j - 1];
                    }
                    strings[i] = str;
                    break;
                }
            }
        }
        n++;
    }

    qsort(strings, 20, sizeof(string_), cmp2);

    for (int i = 0; i < 20; i++) {
        puts(strings[i].str);
    }

    return 0;
}

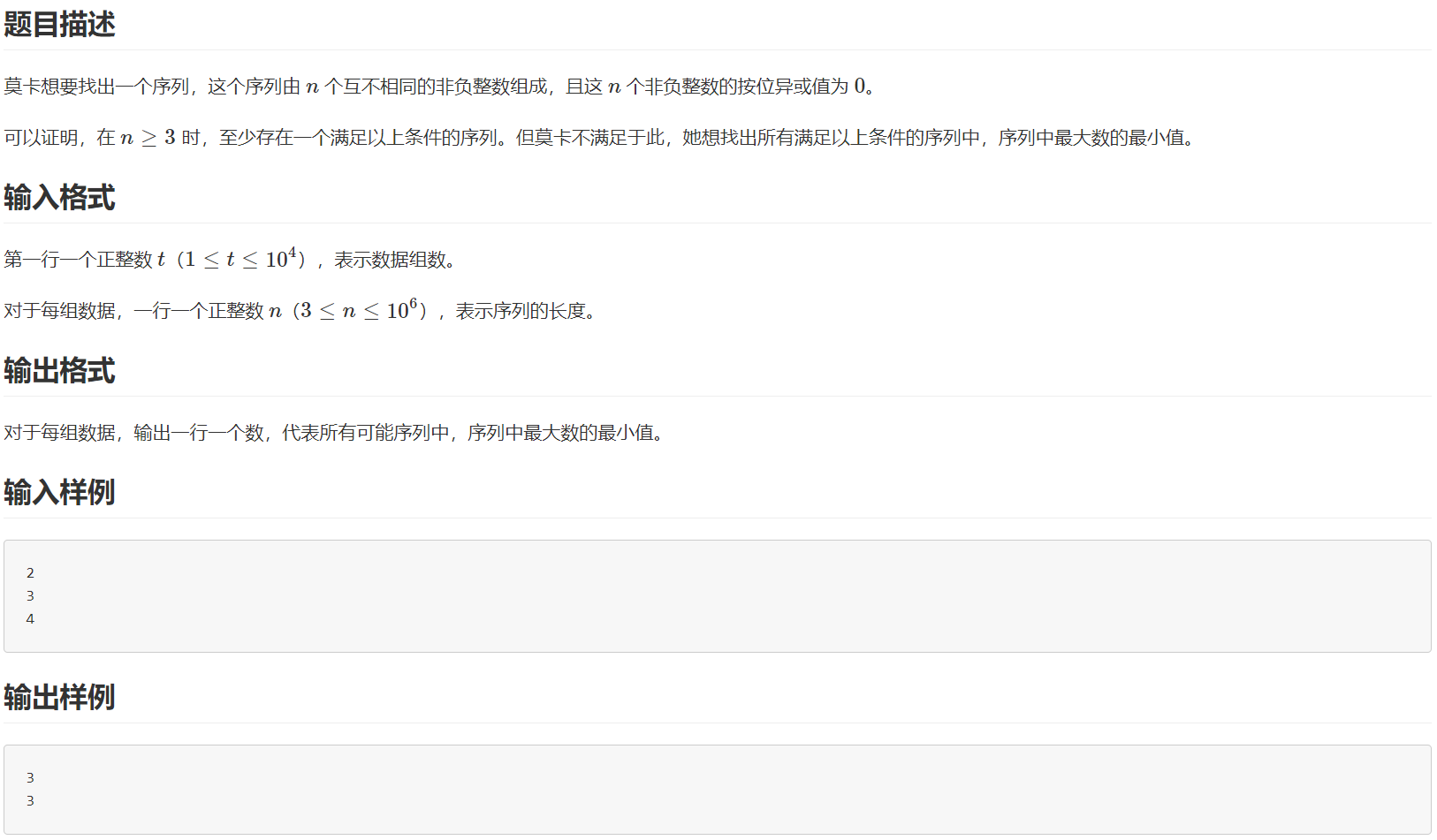
I 莫卡与异或

本次上级赛最喜欢的一道题

原题如下

2024ALC1I

你需要知道

  • 位运算
  • 一些与二进制有关的东西

思路分析

这道题还是挺有意思的，当然这是因为本人水平刚好够到，所以觉得挺有启发性

首先看题目要求，找到n个互不相同的数的序列，按位异或值为0，要求求所有序列中最大数的最小值

好，打住

求最值，即降低了本题难度，明确答案，给了方向性

由于n个数互不相同，在不考虑异或条件下，不难想到最合适的情况为0~n，最小值为n

但是这种情况肯定不能都会满足，而且题目中明确说，而恰恰在3以内的数是解题的关键点

一眼肯定看不出来，先列举一些数字进行观察

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
0       0       0
1       1       1
10      2       01
11      3       11
100     4       001
101     5       101
110     6       011
111     7       111
1000    8       0001
1001    9       1001
1010    10      0101
1011    11      1101
1100    12      0011
1101    13      1011
1110    14      0111
1111    15      1111
10000   16      00001
10001   17      10001
二进制  十进制  按位对齐二进制

列举到这里，够用了，仔细观察，按照最小单元划分按位异或后值恒为0的连续数序列（先分析离散只会导致里结果更远）

发现最小划分方案为四个一组，可以如下两种情况划分（下面只画按位对齐二进制）

偏移量为0（这里偏移量指的是相距最优-最小值为n-情况的整体数列偏移量）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
0
1
01
11
---
001
101
011
111
---
0001
1001
0101
1101
----
0011
1011
0111
1111
----
00001
10001
...
按位对齐二进制

偏移量为2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
(0)
(1)
---
01
11
001
101
---
011
111
0001
1001
----
0101
1101
0011
1011
----
0111
1111
00001
10001
-----
...
按位对齐二进制

以上是不加损耗的偏移（不加损耗指的是全连续，无需考虑填补项凑条件）

光从上面两种情况分析，就已经能得到两种情况的答案了

  • 当(n & 3) == 0时，也即n为4的倍数时，直接使用第一种偏移情况，为最优解
  • 当(n & 3) == 1时，也即n为4的倍数余1时，可以直接使用第二种偏移情况，余数即添加为了偏移去掉的最开始的0，因为0是所有数里面添加减少都无损的，为最优解

那么另外两种情况能不能也参考这个思路走的，很自然bushi，于是顺理成章，来研究一下偏移量分别为1和3的情况

偏移量为1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
0
-
1
01
11
001
---
101
011
111
0001
----
1001
0101
1101
0011
----
1011
0111
1111
00001
10001
按位对齐二进制

没有很多参考意义，因为每四个一组都存在按位异或后有二进制为不为0的情况

偏移量为3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
(0)
(1)
(01)
--
11
001
101
011
---
111
0001
1001
0101
----
1101
0011
1011
0111
----
1111
00001
10001
...
按位对齐二进制

依旧没有进步，至此移位的探索已经分析完了，目前还有两种情况没有解决，先来看与(n & 3) == 1相对称的(n & 3) == 3，因为这两个余数刚好凑整4，可以知道，是在相同情况下的变式

当(n & 3) == 3时，首先通过前面两种偏移可以处理整除4的部分的所有数字序列，相当于只需要处理剩下3个余数的位置了，因为要求获得最小值，所以尽量在小数上下功夫，对于整除四的部分，先将整体偏移四位，得到

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
(0)
(1)
(01)
(11)
---
001
101
011
111
---
0001
1001
0101
1101
----
0011
1011
0111
1111
----
00001
10001
...
按位对齐二进制

现在只需要从最前面删掉的四个中找3个数使得满足这3个数按位异或为0即可，非常容易，只需要去掉0即可，可以不难发现这是唯一最优解法，所以此时得到结论

  • 当(n & 3) == 3时，也即n为4的倍数余3时，可以使用第一种偏移情况，在次基础上加4个偏移量空出前4个数字可供调度，由于0对于按位异或毫无影响，前四个只需要去掉0即可得到最优序列。

最难的是(n & 3) == 2的情况，有上面的基础，还是老样子，扣掉4的整数倍，但是这一次我们需要保留6个数，因为n=2已经被题目贴心排除了(bushi)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
(0)
(1)
(01)
(11)
---
001
101
011
111
---
0001
1001
0101
1101
----
0011
1011
0111
1111
----
00001
10001
...
按位对齐二进制

这样子，现在需要找到6个数，使得6个数之间按位异或值为0，不要被前面4个数诱惑，因为前面4个数还有比直接加上凑6更大的用处，为后面两个数打基础，补弱，这里先考虑比较简单的情况，当n = 10时

1
2
3
4
5
6
7
8
9
10
11
12
(0)
(1)
(01)
(11)
---
001
101
011
111
---
...
按位对齐二进制

列举到这里已经够用了，为了找最优解，先直接添加与最后的011和111相邻的两个数0001和1001

1
2
3
4
5
6
7
8
9
10
11
12
13
14
(0)
(1)
(01)
(11)
---
001
101
011
111
---
0001
1001
...
按位对齐二进制

此时发现第一位满足不了题意了，为了找到最优解，当然不会选择往后选更大的数，由于只是第一位出现异常，前面4个数可以派上用处了，直接看如下选择方案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
(0)
(1)
01
11
---
001
101
011
111
---
0001
1001
...
按位对齐二进制

这样就补齐第一个了，可是不是还少了两个嘛，这次继续前面的模式，往后面找一个数0101

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(0)
(1)
01
11
---
001
101
011
111
---
0001
1001
0101
...
按位对齐二进制

好的，第二位也异常了，没事，调度前面的变成

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(0)
1
01
(11)
---
001
101
011
111
---
0001
1001
0101
...
按位对齐二进制

完美配位，剩下一个数不用说找0

可能你会想，这不就结束了嘛？答案就是n + 2打错特错，这样你会得到0.4分WA的好成绩，为什么跳过了更小的6先来讨论10的情况了呢？观察n = 6，沿用之前的方案，这次考虑偏移量为2

1
2
3
4
5
6
7
8
9
10
11
(0)
(1)
---
01
11
001
101
---
011
111
按位对齐二进制

后面两个数第一位异常，去掉更大的数

1
2
3
4
5
6
7
8
9
10
(0)
(1)
---
01
11
001
101
---
011
按位对齐二进制

发现了么，第三位，也就是高位出现问题了，但是高位不可能由前几个数补，所以这就是6和10不一样的地方，6涉及进位问题，于是必须去掉一个高位，且保证高位的1能够被前面的数补，得到

1
2
3
4
5
6
7
8
9
10
(0)
(1)
---
01
11
001
(101)
---
011
按位对齐二进制

添加1和0

1
2
3
4
5
6
7
8
9
10
0
1
---
01
11
001
(101)
---
011
按位对齐二进制

完成，其它情况类似，不放心读者自行列举，另一类答案n + 3

综合一下即可得到如下代码

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/* 
 Author: 王宇祯
 Result: AC	Submission_id: 6345044
 Created at: Sat Sep 14 2024 20:28:39 GMT+0800 (China Standard Time)
 Problem_id: 8192	Time: 86	Memory: 3492
*/

#include<bits/stdc++.h>
using namespace std;

int main() {
    int t;
    scanf("%d", &t);
    while (t--) {
        int n;
        scanf("%d", &n);
        int mod = n & 3;
        switch (mod) {
            case 0:
                cout << n - 1 << endl;
                break;
            case 1:
                cout << n << endl;
                break;
            case 2:
                if (__builtin_popcount(n + 2) == 1)
                    cout << n + 3 << endl;
                else
                    cout << n + 2 << endl;
                break;
            case 3:
                cout << n << endl;
                break;
        }
    }
    return 0;
}
  • __builtin_popcount(n + 2) 返回n + 2二进制数中数位为1的个数

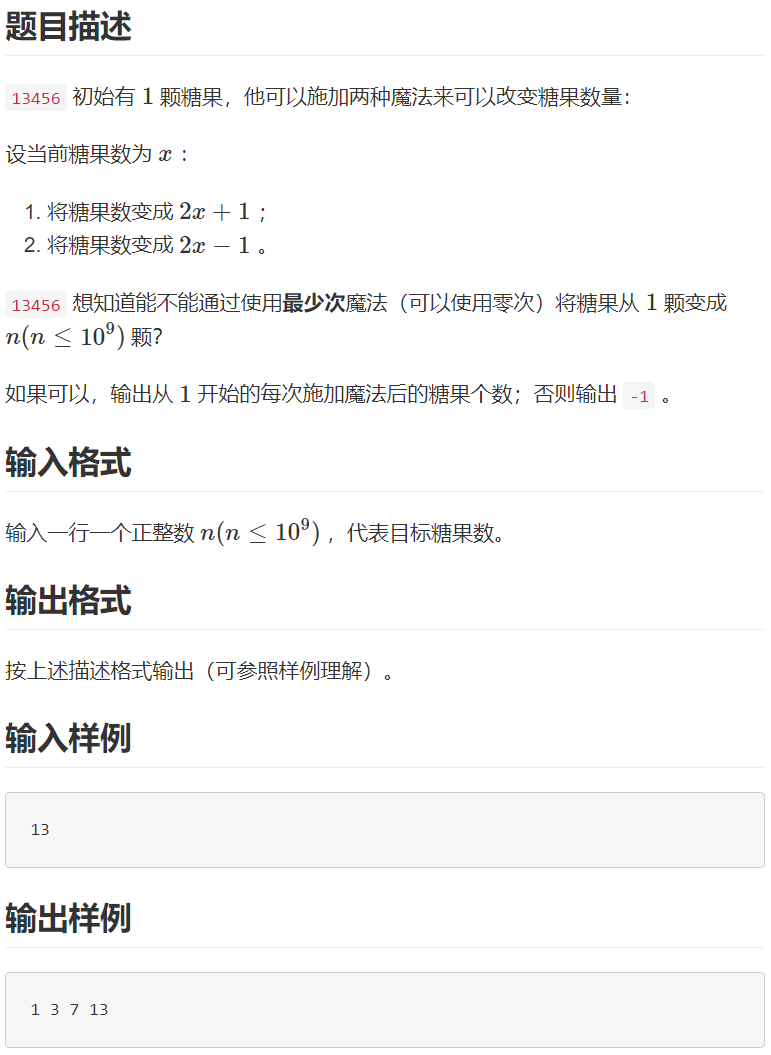
J 魔法糖果

很好玩的一道题

原题如下

2024ALC1J

你需要知道

  • 位运算

思路分析

怎么想到用位运算呢？

一方面是，出题人很喜欢考位运算，不管是从前面类似好玩的I题来看，还是各种大佬的标程（J题标程没参考的前提下），发现这次上机赛有点青睐位运算。或者说是二进制？

再而

仔细观察题目的两种变换方式，发现都与幂2与差1有关，经典对于二进制高度相关的两个数

分析到现在，开始进入正题

  • 2 * x + 1效果是在现有二进制位的基础上，在第0位的1前面添加一个二进制1
  • 2 * x - 1效果是在现有二进制位的基础上，在第0位的1前面添加一个二进制0

之所以说是在第0位的1前面是因为怕位数有歧义，另外也是强调运算的特点，不动第0位

不难发现，第0二进制位永远为1，所以所有(n & 1) == 0的情况都无法满足，输出-1

下面讨论可以满足的情况，根据运算的特点，不难想到只需要将目标数字写成二进制位后，忽略第一位，按照从左到右依次进行相应运算即可，比如是1就对应2 * x + 1，是0就对应2 * x - 1

别忘了每进行一次运算都要输出结果，最开头的1在确认存在满足方案后也要输出！

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/* 
 Author: 王宇祯
 Result: AC	Submission_id: 6345154
 Created at: Sat Sep 14 2024 20:39:36 GMT+0800 (China Standard Time)
 Problem_id: 8181	Time: 17	Memory: 3520
*/

#include<bits/stdc++.h>
using namespace std;
// 位运算

int main() {
    int n;
    cin >> n;
    int now = 1;
    if (n & 1) {
        int flag = 0;
        for (int i = 31; i >= 1; i--) {
            if (flag) {
                if ((n >> i) & 1) { // 第i + 1位为1
                    now = now * 2 + 1;
                    printf("%d ", now);
                } else {
                    now = now * 2 - 1;
                    printf("%d ", now);
                }
            } else {
                if ((n >> i) & 1) { // 第i + 1位为1
                    flag = 1;
                    printf("%d ", now);
                    now = now * 2 + 1;
                    printf("%d ", now);
                }
            }
        }
    } else {
        cout << -1 << endl;
    }
    return 0;
}
  • 标题: 2023级算法C1上机赛
  • 作者: Tengpaz
  • 创建于 : 2024-09-14 17:02:36
  • 更新于 : 2024-10-07 11:19:51
  • 链接: https://qinaida.cn/tengpaz/2024/09/14/2023级算法C1上机赛/
  • 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
评论
目录
2023级算法C1上机赛
  1. 2023级软院学生第一次上机赛习题讲解
    1. 补题情况
    2. C 最长的姓名
      1. 原题如下
      2. 你需要知道
      3. 解题思路
      4. 插入排序&内存压缩
      5. 多关键字
      6. AC代码
    3. I 莫卡与异或
      1. 原题如下
      2. 你需要知道
      3. 思路分析
      4. AC代码
    4. J 魔法糖果
      1. 原题如下
      2. 你需要知道
      3. 思路分析
      4. AC代码